The Simple Bi-directional Wave, as described thus far, is fundamentally a collection of [x, y] integer data points, that are generated by the FOD number set and the performance of several subsequent mathematical operations. By connecting these points with straight line segments we are inferring that some piecewise linear process is responsible for filling in the gaps between integers, creating a continuous function over the domain defined by these endpoint integers. However, we have yet to define such a function mathematically - a necessary process if we are to correctly expand the Simple Bi-directional Wave into the Tri-Level Complex Wave, or 384 number data set.
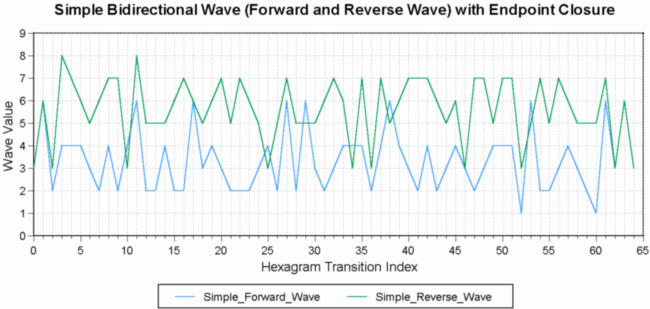
Fig. 3 shows the Simple Bi-directional Wave in its final form. The forward and reverse waves are properly superimposed with the correct endpoint closure, and the data set integers are connected with straight-line segments. Note that the primary closures occur at transition index 1 and index 62, with secondary closures and index 63 and 64. A primary endpoint closure, in this context, is simply the first endpoint closure point as seen from within the bi-directional wave envelope (area enclosed by the double waveform), whereas a secondary endpoint closure point would be all subsequent points of closure. The notion of primary and secondary wave closure is introduced here because it will be used later when the trigramatic and hexagramatic waves are generated and then indexed with the linear wave.
Although Fig. 3 shows the properly superimposed forward
and reverse waves, there is nothing in the graph that provides this sense
of directed flow, except the wave labeling. Fig. 4 introduces, for the
first time, vector representation of the forward and reverse wave segments,
providing a visual image of wave directed flow. This graph shows the forward
and reverse waves engaged a continuously flowing process - forward wave
flows into the reverse wave, and the reverse wave flows back into the forward
wave. This dynamic and continuous cycle is akin to the flow from Yin to
Yang, Yang to Yin, expressed in the well-known Yin-Yang symbol. It is also
similar to a process that is described in quantum theory, as the flow of
matter to energy, energy to matter, in a continuous and never-ending cycle.
Fig. 4 can be then viewed as a continuously flowing counter-clockwise loop
- always in motion, and always changing. So how is this process to be expressed
mathematically so that these principles are preserved, and so they might
be expanded into a form of higher ordered expression? This is where the
principles of vector mathematics can serve the process well.
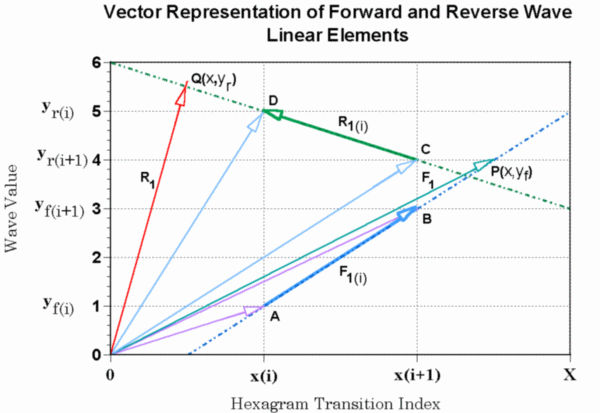
The graph in Fig. 5 shows the generalized form of forward
and reverse wave linear elements, expressed as vectors 
for the forward wave segment, and 
for the reverse wave segment. The subscript 1 in this vector notation signifies
that this vector is a first order element (i.e. a linear wave element
as opposed to a trigramatic or hexagramatic element), and
the 
subscript
signifies that this segment is the i-th element of the forward and
reverse wave line segment set. The vectors 0A, 0B, 0C,
and 0D are construction vectors for 
and 
,
whereas vectors 0P and 0Q are variable, or parametric vectors
that map the lines along which
and 
lie.
In this graph, the x-axis values correspond to
the FOD transitions, with 
or
being the i-th FOD transition, and 
or 
being the i-th +1 transition, and together they define the domain
of the linear bi-directional wave elements. The y-axis values in
Fig. 5 correspond to the magnitude of the forward and reverse waves, with 
and 
being the i-th integer values (at x = i) of the forward and
reverse waves respectively. The values 
and 
are the i-th +1 integer values (at x = i+1) of the forward
and reverse waves respectively. These y values define the range
of the Simple Bi-directional Wave, from the forward and reverse
wave values: 
.
The subscript i is important here because it establishes the boundary
conditions (x domain) within which each line segment expresses itself.
This subscript is associated with the linear wave, and is a function
of the independent variable x. Let us define X = {x} as the
set of all positive real numbers in the domain of the TWZ data set, 
and the subscript i as a function of x :
[11]Where int() indicates the argument x is rounded down to its integer value.
The vector notation view of Fig. 5, can be viewed as an abstraction for motion or flow. With this notation we leave the realm of classical geometry, or statics, and enter the realm of kinematics - the path of a moving point. When sketching a line or a curve with pencil, for example, the point of the pencil occupies a unique position on the line or curve at any given instant of time. Then as we move our hand, the position of the pencil point changes in time and traces the line or curve. This is essentially how vector mathematics serves the foundation and spirit of the 384 number data set development. Similarly,
the Simple Bi-directional Wave describes the path
of a moving point, a counter-clockwise flow of some entity, be it matter,
energy, photon, graviton, novelton,
or eschaton.
In this dynamic or kinematic process, we will make use of the notion of
the parameter.
The parameter has been described by Anderson [9]
as an independent variable which serves to determine the coordinates
of a point or describe its motion. This is the notion that will be
used here, to establish the vector parametric equation of the straight
line in a plane. Again, according to Anderson, the parametric form tells
us where the point goes, when it gets there as well as the curve along
which it travels. Before this parameterization is begun, however, vectors 
and 
must first be defined mathematically.
(1) Forward Wave Vector Equations
Referring to Fig. 5, the forward wave vector 
,
for the i-th transition element can be expressed as directed line
segment AB:
[12]
[13]Rearranging equation [13]:
[14]Substituting standard form:
[15]Which reduces to:
[16]
(2) Reverse Wave Vector Equations
The reverse wave vector 
,
for the i-th transition element can be expressed as directed line
segment C:
[17]and the vector 0D is expressed:
[18]Rearranging equation [18]:
[19]
Substituting standard form:
[20]
[21]
With the derivation of equation [16] and [21], we have
now defined the generalized forward and reverse wave vectors mathematically.
These vector definitions will be used to formulate the vector parametric
equations of the generalized line segment, the basis for the Simple
Bi-directional Wave and the wave expansions that follow.
(3) The Linear Bi-directional Wave
The Simple Bi-directional Wave is all that we have thus far defined or described; but this wave forms the basis for the Linear, Trigramatic, and Hexagramatic waves which are all products of the expansion of this basic building block. The first step in the process of wave expansion and combination that eventually leads to the 384 number data set is the generation of the Linear Bi-directional Wave. This wave is produced from the Simple Bi-directional Wave (SBW) by simple concatenation - i.e. inserting five copies of the SBW end-to-end with the original, and producing six SBW cycles. According to McKenna, the Linear Wave is an expression of the six lines that define each I-Ching hexagram - The SBW then represents one line of the hexagram, and there are six SBW connected end-to-end to form the Linear Bi-directional Wave (LBW). Fig. 6 is a graph of this expanded SBW, or Linear Bi-directional Wave (LBW), and shows the concatenation process that expands the SBW (64 values, excluding zero) into the LBW (384 values, excluding zero). Although this graph does not show the vector structure of Fig. 4 (to avoid crowding the graph), it is implied here. The LBW therefore expresses the same process of directed flow as does the SBW, a counter-clockwise flow of some point entity along the path traced by the forward and reverse waves in Fig. 6.
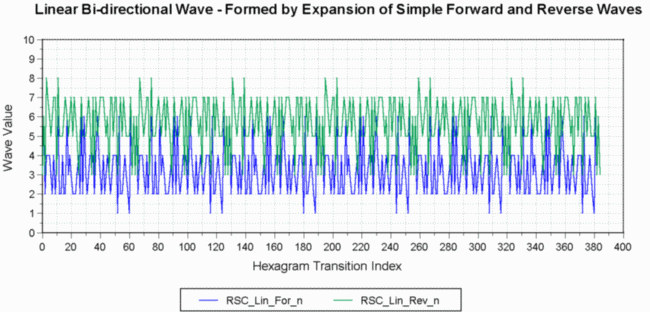
The concatenation process that produces the LBW can be expressed mathematically as follows:
For: 
[22]and for: 
[23]Where: 
(pronounced lin of i) is the value of the forward or reverse linear
wave at transition point i or at 
;
and 
is the value of the forward or reverse linear wave at 
,
where 
is the remainder when i is divided by 64.
The Linear Bi-directional Wave (LBW) will now be
expressed mathematically, and expanded into the Trigramatic Bi-directional
Wave (TBW), and Hexagramatic Bi-directional Wave (HBW), using
mathematics derived from the vector parametric equation of the straight
line.
[continue] [results & conclusions] [index] [hyperborea] [back]